회로 토폴로지 - 기본 개념

전기 회로는 전류가 흐를 수 있는 일련의 장치(요소) 및 연결 와이어입니다. 전기 회로의 모든 요소는 공유합니다. 패시브와 액티브에서.

활성 요소는 다양한 유형의 에너지(기계적, 화학적, 빛 등)를 전기 에너지로 변환합니다. 수동 장치에서 전기 에너지는 다른 유형의 에너지로 변환됩니다. 활성 요소를 소스라고 하고 수동 요소를 소비자 또는 수신기라고 합니다.

회로 이론에서는 전기 요소의 이상화된 모델이 고려됩니다. 이렇게 하면 요소에 대한 설명이 최대한 간단해집니다. 보다 복잡한 실제 요소는 이상화된 요소 집합에서 모델링됩니다.

전기 회로의 주요 수동 소자는 저항(저항 소자), 인덕터(유도 소자) 및 커패시터(용량 소자)입니다. 요소는 전기 회로에 설치되어 주어진 값과 모양의 전압과 전류를 생성합니다(참조 — 전기 회로 및 그 요소).

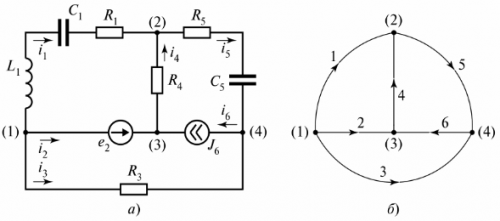
전기 회로는 분기와 노드로 구성됩니다. 나뭇가지 - 이것은 동일한 전류가 흐르는 전기 회로(회로)의 한 부분입니다. 매듭 - 3개 이상의 분기 연결. 전기 다이어그램에서 노드는 점으로 표시됩니다(그림 1).

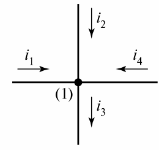
쌀. 1. 다이어그램에서 노드 정의

필요한 경우 다이어그램의 노드는 왼쪽에서 오른쪽으로 위에서 아래로 번호가 매겨집니다.

무화과에서. 그림 2는 전류 iC가 흐르는 저항 용량성 분기를 보여줍니다.

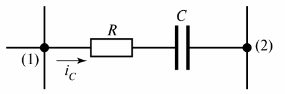
쌀. 2. 저항 용량 분기

분기의 또 다른 정의가 주어질 수 있습니다. 두 개의 인접한 노드(그림 2의 노드 (1) 및 (2)) 사이의 회로 섹션입니다.

체인 전기 회로에 닫힌 경로가 있습니까? 저항이 무한대인 조건 분기를 포함하여 모든 분기로 회로를 닫을 수 있습니다.

무화과에서. 그림 3은 세 개의 분기로 구성된 분기 전기 회로를 보여줍니다.

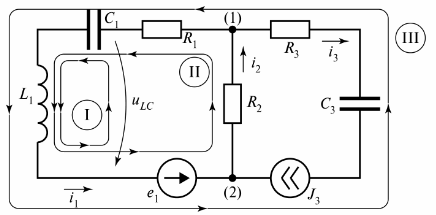
쌀. 3. 두 개의 회로가 있는 전기 회로

다이어그램은 세 개의 회로를 보여 주며 회로 I은 무한 저항 분기에 의해 닫힙니다. 이 분기는 전압 tiLC로 표시됩니다.

그림의 회로에 대해 3 실제 분기 또는 조건부 분기로 닫히는 많은 루프를 구성할 수 있지만 전기 노이즈 계산에는 «독립 루프» 개념이 사용됩니다. 독립 회로 루프의 수는 항상 계산에 필요한 최소값으로 설정됩니다.

독립 회로는 항상 닫혀 있지만 저항이 무한대가 아닌 분기를 가지며 각 독립 회로에는 다른 회로에 포함되지 않은 분기가 하나 이상 포함됩니다. 복잡한 전기 회로의 경우 회로도를 사용하여 독립 회로의 수를 결정할 수 있습니다.

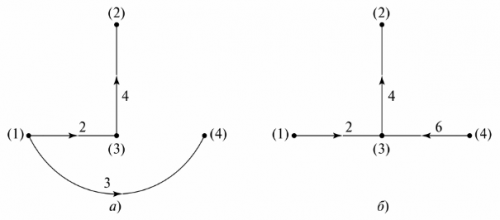
회로도에서 각 분기가 선분으로 대체되는 회로의 조건부 표현이 호출됩니다. 지점의 항목은 표시되지 않습니다. 예를 들어, 도 1에서. 그림 4는 분기 회로와 그 다이어그램을 보여줍니다.

쌀. 4. 분기 전기 회로: a — 회로도, b — 다이어그램

다이어그램의 다이어그램을 만들려면 노드에 요소를 지정하지 않고 분기선으로 노드를 연결해야 합니다. 가지에는 번호가 매겨져 있고 가지에 흐르는 흐름의 방향은 화살표로 표시되어 있습니다. 그래프 자체에는 물리적인 의미가 없지만 독립적인 등고선의 수와 유형을 결정하는 데 사용할 수 있습니다. 이를 위해 "그래픽 트리"가 준비됩니다.

그래픽 트리 폐쇄 루프가 발생하지 않는 방식으로 노드가 분기로 연결된 회로의 그래프를 나타냅니다. 그래픽 트리를 표시하기 위한 몇 가지 옵션이 있을 수 있습니다. 무화과에서. 도 5는 도 5의 회로에 대한 2개의 가능한 옵션을 도시한다. 4.

쌀. 5. 체계의 그래픽 트리

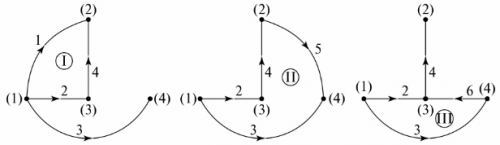
그래프 트리에서 누락된 가지의 수는 회로의 독립 루프 수와 같습니다. 이 예에서는 세 개의 분기, 세 개의 독립 루프입니다. 독립 루프의 구성은 그래프 트리의 노드와 그래프 트리에 지정되지 않은 분기를 순차적으로 연결하여 얻을 수 있습니다. 예를 들어, 그림의 그래프 트리의 경우 5, 독립 윤곽선은 그림 5에 나와 있습니다. 6.

쌀. 6. 그래프 트리를 통한 독립 등고선 결정

회로 계산을 위한 독립 회로 구성 옵션 선택은 회로 분석 중에 수행됩니다. 계산이 가능한 한 간단하도록 이러한 윤곽선을 선택해야 합니다. 시스템의 종속 방정식의 수는 최소화됩니다.

위상 방정식은 회로의 전압과 전류 사이의 관계를 설정하며 방정식의 수와 유형은 분기에 포함된 요소에 의존하지 않습니다. 위상 방정식에는 다음으로 구성된 방정식이 포함됩니다. Kirchhoff의 법칙에 따르면.