단일 공급 장치가 있는 비분지형 및 분기형 선형 전기 회로

e의 소스와 함께 많은 수의 수동 요소가 있는 경우. 등. c. 전기 회로를 형성하고 서로 다른 방식으로 상호 연결될 수 있습니다. 이러한 연결에는 다음과 같은 일반적인 체계가 있습니다.

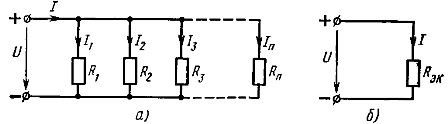
요소의 직렬 연결 이것은 가장 간단한 연결입니다. 이 연결을 통해 동일한 전류가 회로의 모든 요소에 흐릅니다. 이 구성표에 따르면 회로의 모든 수동 요소를 연결할 수 있으며 회로는 분기되지 않은 단일 회로가 되거나(그림 1, a) 다중 회로 회로 요소의 일부만 연결될 수 있습니다. 연결.

n개의 요소가 직렬로 연결되고 동일한 전류 I가 흐르는 경우 회로 단자의 전압은 직렬로 연결된 n개의 요소의 전압 강하의 합과 같습니다.

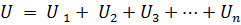
또는:

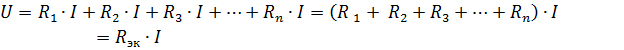
여기서 Rek는 등가 회로 저항입니다.

따라서 직렬로 연결된 수동 소자의 등가 저항은 이러한 소자의 저항의 합과 같습니다. 전기 구성표(그림.1, a) 등가 저항 Rek를 갖는 하나의 요소로 구성된 등가 회로를 제시할 수 있습니다(그림 1, b).

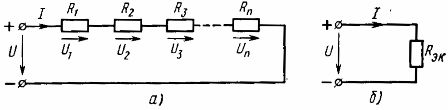
쌀. 1. 선형 요소의 직렬 연결 방식(a) 및 그와 동등한 방식(b)

주어진 전원 전압과 요소 저항에서 요소가 직렬로 연결된 회로를 계산할 때 회로의 전류는 옴의 법칙에 따라 계산됩니다.

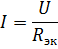
k 번째 요소의 전압 강하

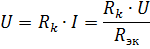
이 요소의 저항뿐만 아니라 등가 저항 Rek, 즉 회로의 다른 요소의 저항에도 의존합니다. 이것은 요소의 직렬 연결의 중요한 단점입니다. 제한적인 경우 회로의 어떤 요소의 저항이 무한대가 되면(개방 회로) 회로의 모든 요소의 전류는 0이 됩니다.

직렬로 연결하면 회로의 모든 요소의 전류가 동일하므로 요소의 전압 강하 비율은 이러한 요소의 저항 비율과 같습니다.

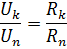
요소의 병렬 연결 - 이것은 회로의 모든 요소에 동일한 전압이 적용되는 연결입니다. 병렬 연결 방식에 따르면 회로의 모든 수동 요소(그림 2, a) 또는 일부만 연결할 수 있습니다. 각 병렬 연결 요소는 별도의 분기를 형성합니다. 따라서 그림 1에 표시된 요소를 병렬로 연결한 회로는 다음과 같습니다. 2, a는 단순한 회로이지만(2개의 노드만 포함하므로) 동시에 분기됩니다.

쌀. 2. 선형 요소의 병렬 연결 방식(a) 및 그와 동등한 방식(b)

각 병렬 분기에서 전류

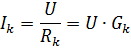
여기서 Gk는 k번째 분기의 전도도입니다.

에서 키르히호프의 제1법칙

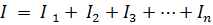
또는

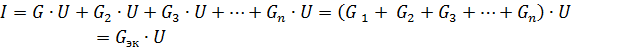
여기서 Gec은 등가 회로 컨덕턴스입니다.

따라서 수동 소자가 병렬로 연결될 때 등가 컨덕턴스는 이러한 요소의 컨덕턴스의 합과 같습니다... 등가 컨덕턴스는 항상 병렬 분기의 컨덕턴스보다 큽니다. 등가 전도도 GEK는 등가 저항 Rek = 1/Gek에 해당합니다.

그런 다음 그림에 표시된 등가 회로. 2, a는 그림과 같은 형식을 갖습니다. 2, b 요소가 병렬로 연결된 회로의 분기되지 않은 부분의 전류는 옴의 법칙에 따라 이 회로에서 결정할 수 있습니다.

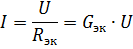
따라서 공급 전압이 일정하면 병렬로 연결된 요소의 수가 증가함에 따라 (등가 전도도가 증가함) 회로의 분기되지 않은 부분의 전류 (전원 공급 전류)가 증가합니다.

공식에서

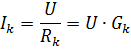
각 분기의 전류는 해당 분기의 컨덕턴스에만 의존하고 다른 분기의 컨덕턴스에는 의존하지 않는다는 것을 알 수 있습니다. 서로 병렬 분기 모드의 독립성은 수동 소자의 병렬 연결의 중요한 이점입니다. 산업 설비에서는 전기 수신기의 병렬 연결이 대부분의 경우에 사용됩니다. 가장 분명한 예는 조명용 전등을 포함하는 것입니다.

병렬 연결에서 동일한 전압이 모든 요소에 적용되고 각 분기의 전류는 해당 분기의 컨덕턴스에 비례하므로 병렬 분기의 전류 비율은 이러한 분기의 컨덕턴스 비율과 같거나 반비례합니다. 그들의 저항의 비율:

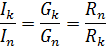
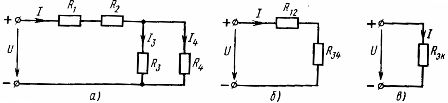
요소의 혼합 연결은 직렬 및 병렬 연결의 조합입니다. 이러한 체인은 다른 수의 노드와 분기를 가질 수 있습니다. 혼합 연결의 예가 다이어그램에 나와 있습니다 (그림 3, a)

쌀. 3. 선형 요소(a)와 그와 동등한 구성(b, c)의 혼합 연결 방식.

이러한 회로를 계산하려면 직렬 또는 병렬로만 연결된 회로 부분의 등가 저항을 연속적으로 결정해야 합니다. 고려된 회로에는 저항 R1 및 R2가 있는 요소의 직렬 연결과 저항 R3 및 R4가 있는 요소의 병렬 연결이 있습니다. 직렬 및 병렬 연결이 있는 회로 요소의 매개 변수 사이에서 이전에 얻은 관계를 사용하여 실제 전기 회로를 등가 회로로 연속적으로 대체할 수 있습니다.

직렬로 연결된 요소의 등가 저항

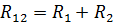
병렬 연결된 요소 R3 및 R4의 등가 저항

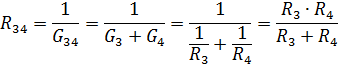
요소 R12 및 R34의 저항을 갖는 등가 회로가 그림 1에 나와 있습니다. 3, 나. R12와 R34의 이 직렬 연결의 경우 등가 저항은

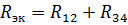
해당 등가 회로가 그림 1에 나와 있습니다. 2, 나. 이 회로에서 전류를 찾아봅시다.

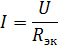
이들은 실제 회로의 요소 R1 및 R2의 공급 전류 및 전류입니다.전류 I3 및 I4를 계산하려면 저항 R34가 있는 회로 섹션의 전압을 결정합니다(그림 3, b).

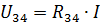
그런 다음 옴의 법칙에 따라 전류 I3 및 I4를 찾을 수 있습니다.

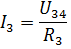
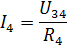
유사한 방식으로 수동 요소의 혼합 연결을 사용하여 여러 다른 전기 회로를 계산할 수 있습니다.

많은 수의 회로 및 e 소스가 있는 복잡한 회로의 경우. 등. c. 그러한 등가 변환이 항상 수행될 수는 없습니다. 그들은 다른 방법으로 계산됩니다.