전기장 속의 전자

전기장에서 전자의 이동은 전기 공학에서 가장 중요한 물리적 과정 중 하나입니다. 그림 이것이 진공 상태에서 어떻게 일어나는지 봅시다. 먼저 균일한 전기장에서 음극에서 양극으로 전자가 이동하는 예를 살펴보겠습니다.

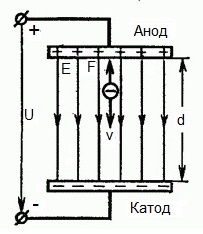
아래 그림은 다음과 같은 상황을 보여줍니다. 전자 무시할 정도로 작은 초기 속도(0에 가까워짐)로 음극(음극)을 떠나 균일한 전기장에서두 전극 사이에 존재.

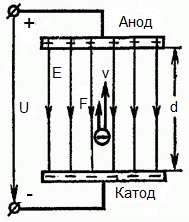
일정한 전압 U가 전극에 가해지고 전기장은 해당 강도 E를 갖습니다. 전극 사이의 거리는 d와 같습니다. 이 경우 전자의 전하와 필드의 강도에 비례하는 힘 F가 필드 측면에서 전자에 작용합니다.

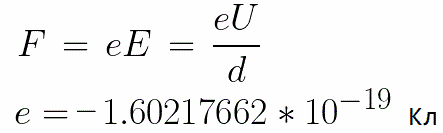
전자는 음전하를 가지므로 이 힘은 전계 강도 벡터 E에 대해 향하게 됩니다. 따라서 전자는 전기장에 의해 그 방향으로 가속됩니다.

전자가 받는 가속도는 전자에 작용하는 힘 F의 크기에 비례하고 전자의 질량 m에 반비례합니다.필드가 균일하기 때문에 주어진 그림에 대한 가속도는 다음과 같이 표현할 수 있습니다.

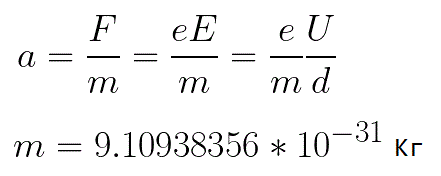
이 공식에서 전자의 전하량과 질량의 비율은 전자의 비전하량이며 물리 상수입니다.

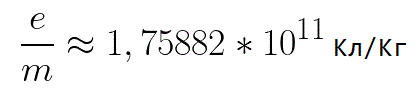
따라서 전자는 초기 속도 v0의 방향이 필드 측면의 힘 F의 방향과 일치하므로 전자가 균일하게 움직이기 때문에 가속 전기장에 있습니다. 장애물이 없으면 전극 사이의 경로 d를 이동하여 특정 속도 v로 양극(양극)에 도달합니다. 전자가 양극에 도달하는 순간 운동 에너지는 다음과 같습니다.

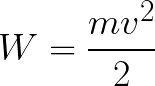
전체 경로 d를 따라 전자는 전기장의 힘에 의해 가속되기 때문에 전기장의 측면에 작용하는 힘이 한 일의 결과로 이 운동 에너지를 얻습니다. 이 작업은 다음과 같습니다.

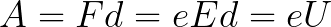
그러면 필드에서 이동하는 전자가 획득한 운동 에너지는 다음과 같이 구할 수 있습니다.

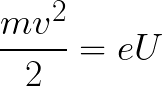
즉, 전위차 U가 있는 지점 사이에서 전자를 가속하는 것은 필드 포스의 작업에 지나지 않습니다.

이러한 상황에서 전자의 에너지를 표현하기 위해 1볼트의 전압에서 전자의 에너지와 같은 "전자 볼트"와 같은 측정 단위를 사용하는 것이 편리합니다. 그리고 전자 전하가 일정하기 때문에 1eV도 일정한 값입니다.

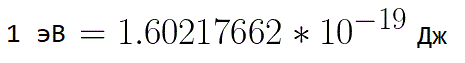
이전 공식에서 가속할 때 통과한 전위차만 알면 가속 전기장에서 이동할 때 경로의 모든 지점에서 전자의 속도를 쉽게 결정할 수 있습니다.

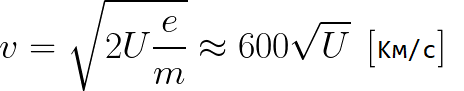
보시다시피 가속 필드에서 전자의 속도는 경로의 끝점과 시작점 사이의 전위차 U에만 의존합니다.

전자가 무시할 수 있는 속도로 음극에서 멀어지기 시작하고 음극과 양극 사이의 전압이 400볼트라고 상상해 보십시오. 이 경우 양극에 도달하는 순간 속도는 다음과 같습니다.

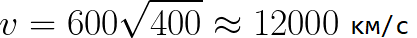
또한 전자가 전극 사이의 거리 d를 이동하는 데 필요한 시간을 결정하는 것도 쉽습니다. 정지 상태에서 균일하게 가속된 모션에서 평균 속도는 최종 속도의 절반인 것으로 밝혀지며 전기장에서 가속 비행 시간은 다음과 같습니다.

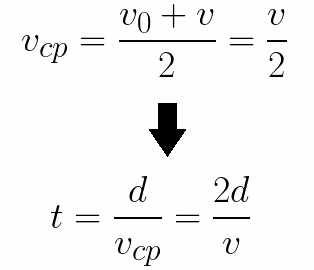
이제 전자가 감속하는 균일한 전기장에서 이동하는 경우를 예로 들어 보겠습니다. 즉, 필드는 이전과 같이 방향이 지정되지만 전자는 양극에서 음극으로 반대 방향으로 이동하기 시작합니다.

전자가 초기 속도 v로 양극을 떠나 처음에 음극 방향으로 움직이기 시작했다고 가정합니다. 이 경우 전기장 측면에서 전자에 작용하는 힘 F는 전기 강도 벡터 E - 음극에서 양극으로 향합니다.

그것은 전자의 초기 속도를 줄이기 시작할 것입니다. 즉, 필드는 전자의 속도를 늦출 것입니다. 이것은 이러한 조건에서 전자가 균일하고 균일하게 천천히 움직이기 시작한다는 것을 의미합니다. 상황은 다음과 같이 설명됩니다. "감속 전기장에서 전자가 움직입니다."

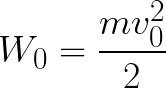
애노드에서 전자는 0이 아닌 운동 에너지로 움직이기 시작했으며 감속 중에 감소하기 시작합니다. 이제 에너지가 전자의 필드에서 작용하는 힘을 극복하는 데 소비되기 때문입니다.

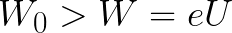
전자가 양극을 나갈 때의 초기 운동 에너지가 전자가 음극에서 양극으로 이동하는 것을 가속하기 위해 필드에 의해 소비되어야 하는 에너지보다 즉시 더 크다면(첫 번째 예에서와 같이) 전자는 거리 d를 이동하고 제동에도 불구하고 결국 음극에 도달합니다.

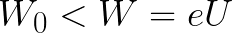
전자의 초기 운동 에너지가 이 임계값보다 작으면 전자는 음극에 도달하지 못합니다. 특정 지점에서 정지한 다음 다시 양극으로 균일하게 가속된 이동을 시작합니다. 결과적으로 필드는 중지 과정에서 소비된 에너지를 반환합니다.

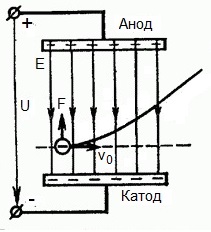
그러나 전자가 전기장의 작용 영역에서 직각으로 속도 v0로 날아간다면 어떻게 될까요? 분명히, 이 영역에서 자기장 측면의 힘은 전자가 음극에서 양극으로, 즉 전계 강도 벡터 E에 대해 향합니다.

이것은 이제 전자가 운동의 두 가지 구성 요소를 가짐을 의미합니다. 첫 번째는 필드에 수직인 속도 v0이고 두 번째는 필드 측면에서 양극을 향한 힘의 작용에 따라 균일하게 가속됩니다.

행동 영역으로 날아간 전자는 포물선 궤적을 따라 움직입니다. 그러나 필드의 작용 영역 밖으로 날아간 후 전자는 직선 궤적을 따라 관성에 의해 등속 운동을 계속할 것입니다.