기자력이란 홉킨슨의 법칙
19세기 후반, 자기 회로의 일반 이론을 발전시킨 영국의 물리학자 존 홉킨슨과 그의 형제 에드워드 홉킨슨은 옴의 법칙과 유사한 "홉킨슨의 공식" 또는 홉킨슨의 법칙이라는 수학 공식을 도출했습니다. 전기 회로 계산).
따라서 옴의 고전법칙이 전류와 기전력(EMF)의 관계를 수학적으로 기술한다면, 홉킨슨의 법칙은 유사하게 자속과 소위 기전력의 관계를 표현한다. 기자력(MDF).

그 결과, 기자력은 자속을 생성하는 전류의 능력을 특징짓는 물리량입니다. 그리고 이와 관련하여 Hopkinson의 법칙은 자기 회로의 MDF가 전기 회로의 EMF와 유사하기 때문에 자기 회로 계산에 성공적으로 사용될 수 있습니다. Hopkinson의 법칙이 발견된 날짜는 1886년으로 간주됩니다.
기자력(MDF)의 크기는 처음에 암페어 단위로 측정됩니다. 전류 또는 전자석이 있는 코일에 대해 이야기하는 경우 계산의 편의를 위해 암페어 단위로 표현을 사용합니다.
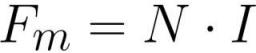
여기에서 Fm은 코일의 기자력[암페어 * 회전], N은 코일의 회전 수[회전], I는 코일의 각 회전에 있는 전류의 양[암페어]입니다.
여기에 자속 값을 입력하면 자기 회로에 대한 홉킨슨의 법칙은 다음과 같은 형식을 취합니다.
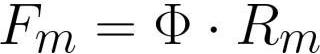
여기서: Fm은 코일의 기자력[암페어 * 회전], F는 자속 [웨버] 또는 [헨리 * 암페어], Rm은 자속 도체의 자기 저항[암페어 * 회전/웨버] 또는 [ 턴 / 헨리] .
홉킨슨 법칙의 텍스트 형식은 원래 다음과 같습니다. 즉, 이 법칙은 회로에서 기자력, 저항 및 자속 간의 관계를 결정합니다.
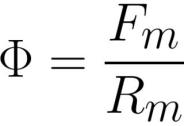
여기서: F는 자속[weber] 또는 [henry * ampere], Fm은 코일의 기자력[ampere * rotation], Rm은 자속 도체의 자기 저항[ampere * rotation / weber] 또는 [ 턴 / 헨리] .
여기에서 사실 기자력(MDF)은 기전력(EMF)과 근본적인 차이가 있다는 점에 주목하는 것이 중요합니다. 기전력(EMF)은 어떤 입자도 자기 플럭스에서 직접 움직이지 않는다는 사실에 있습니다. EMF는 예를 들어 금속 와이어의 전자와 같은 하전 입자의 움직임을 취합니다. 그러나 MDS의 아이디어는 자기 회로 계산 문제를 해결하는 데 도움이 됩니다.
예를 들어, 전체 길이가 동일한 단면적 S의 요크를 포함하고 요크의 재료가 자기 투자율 μ를 갖는 비분기형 자기 회로를 고려하십시오.
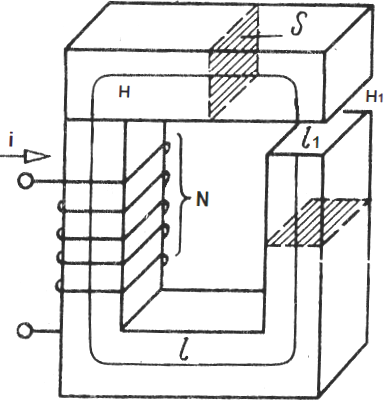
멍에의 틈 - 다른 재료, 투자율 어떤 뮤1. 요크에 놓인 코일은 N 회전을 포함하며 전류 i는 코일의 각 회전을 통해 흐릅니다. 요크의 중심선에 자기장 순환 정리를 적용합니다.
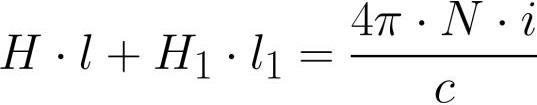
여기에서 H는 요크 내부의 자기장 강도, H1은 갭 내부의 자기장 강도, l은 요크 유도의 중심선 길이(갭 제외), l1은 갭의 길이입니다.
요크 내부와 갭 내부의 자속은 같은 값을 갖기 때문에(자기 유도선의 연속성으로 인해) Ф = BS 및 В = mu * H라고 쓴 후 자기장 강도를 자세히 적어 보겠습니다. , 그리고 이것을 위의 공식으로 대체한 후:
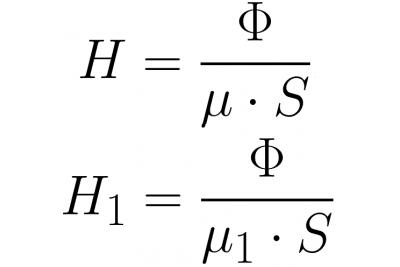
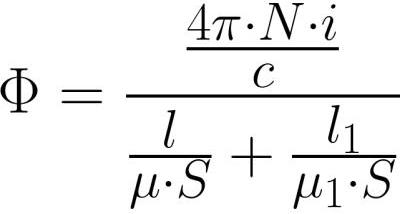
전기 회로에 대한 옴의 법칙의 EMF와 같이 MDS가
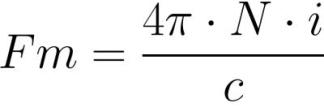
여기서 기전력과 자기저항의 역할을 한다.
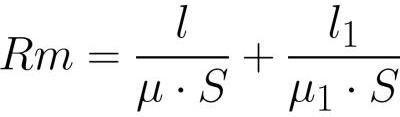
저항의 역할(유추에 의해 고전적인 옴의 법칙으로).
