연속 진동 및 파라메트릭 공명

연속 진동 — 시간이 지나도 에너지가 변하지 않는 진동. 실제 물리적 시스템에는 진동 에너지를 열 에너지로 전환시키는 원인이 항상 있습니다(예: 기계 시스템의 마찰, 전기 시스템의 능동 저항).

따라서 감쇠되지 않은 진동은 이러한 에너지 손실이 보충되는 경우에만 얻을 수 있습니다. 이러한 보충은 외부 소스의 에너지로 인해 자체 발진 시스템에서 자동으로 발생합니다. 연속 전자기 진동은 매우 널리 사용됩니다. 이를 얻기 위해 다른 생성기가 사용됩니다.

(진동하는 원 또는 진자의) 전기적 또는 기계적 진동을 감쇠시키지 않으려면 항상 저항 또는 마찰 손실을 보상해야 합니다.

예를 들어, 코일의 전류를 주기적으로 증가시켜 커패시터의 전압 진폭을 유지하는 교류 EMF로 발진 회로에 작용할 수 있습니다.또는 비슷한 방식으로 진자를 밀어서 조화롭게 흔들리게 할 수 있습니다.

아시다시피 발진 회로의 코일 자기장의 에너지 크기는 다음과 같은 관계로 인덕턴스와 전류와 관련됩니다 (두 번째 공식은커패시터 전기장의 에너지 동일한 윤곽 윤곽)

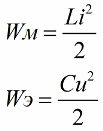
첫 번째 공식에서 교류 EMF 회로에 작용하는 코일의 전류를 주기적으로 늘리면 (공식에서 두 번째 요소 인 전류를 늘리거나 줄임으로써) 주기적으로이 회로에 에너지를 보충한다는 것이 분명합니다.

자연적인 자유 진동, 즉 공진 주파수에서 엄격하게 회로에 작용하면 공진 주파수에 있기 때문에 전기 공진 현상이 발생합니다. 진동 시스템 공급되는 에너지를 가장 집중적으로 흡수합니다.

그러나 주기적으로 두 번째 요소(전류 또는 전압이 아님)가 아니라 첫 번째 요소인 인덕턴스 또는 커패시턴스를 변경하면 어떻게 될까요? 이 경우 회로의 에너지도 변경됩니다.

예를 들어 주기적으로 코어를 코일 안팎으로 밀거나 축전기를 안팎으로 밀고 나갑니다.유전체, — 우리는 또한 회로의 에너지에서 매우 명확한 주기적인 변화를 얻습니다.

코일 인덕턴스의 단위 변화에 대해 이 위치를 씁니다.

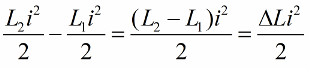
회로 스윙의 가장 두드러진 효과는 인덕턴스 변경이 적시에 이루어지는 경우입니다. 예를 들어, 어떤 순간에 동일한 회로를 취하고 어떤 전류가 이미 흐르고 있을 때 코일에 코어를 도입하면 에너지는 다음과 같은 양만큼 변경됩니다.

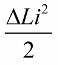
이제 회로 자체에 자유 발진이 나타나도록 놔두십시오. 그러나 1/4 기간 후에 에너지가 커패시터로 완전히 전달되고 코일의 전류가 0이되는 순간 코일에서 코어를 갑자기 제거합니다. 인덕턴스 원래 상태인 초기 값 L로 돌아갑니다. 코어가 제거될 때 자기장에 대한 작업이 필요하지 않습니다. 따라서 코어를 코일에 밀어 넣었을 때 우리가 작업한 이후로 회로에 에너지가 공급되었으며 그 값은 다음과 같습니다.

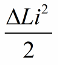
1/4 기간이 지나면 커패시터가 방전되기 시작하고 그 에너지는 다시 코일의 자기장 에너지로 변환되며 자기장이 진폭에 도달하면 코어를 다시 세게 누릅니다. 다시 인덕턴스가 증가하여 같은 양만큼 증가했습니다.

그리고 다시 제로 전류에서 인덕턴스를 원래 값으로 되돌립니다. 결과적으로 각 반주기의 에너지 이득이 저항 손실을 초과하면 루프의 에너지가 항상 증가하고 진동 진폭이 증가합니다. 이 상황은 불평등으로 표현됩니다.

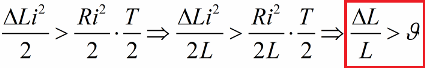
여기에서 우리는 이 부등식의 양쪽을 L로 나누고 로그 감소의 특정 값에 대한 점프에 의한 파라메트릭 여기 가능성에 대한 조건을 적었습니다.

주기당 인덕턴스(또는 커패시턴스)를 두 번 변경하는 것이 좋습니다. 따라서 파라미터 변경 주파수(파라메트릭 공진 주파수)는 발진 시스템의 고유 주파수의 두 배가 되어야 합니다.

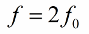
따라서 EMF 또는 전류를 직접 변경할 필요없이 회로의 진동 여기 경로가 나타났습니다.회로의 초기 변동 전류는 항상 어떤 식으로든 존재하며 이는 대기의 무선 주파수 진동으로 인한 간섭을 고려하지도 않습니다.

인덕턴스 (또는 커패시턴스)가 점프에서 변경되지 않고 조화롭게 변경되면 진동 발생 조건이 약간 다르게 보입니다.

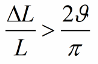
커패시턴스와 인덕턴스는 진자의 질량이나 스프링의 탄성과 같은 회로 매개변수이므로 진동을 여기시키는 방법을 파라메트릭 여기라고도 합니다.

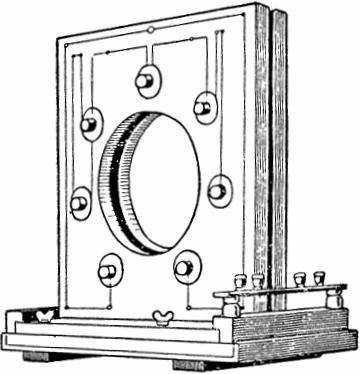
이 현상은 20세기 초 소련의 물리학자 만델스탐과 파팔렉시가 발견하고 실제로 연구했습니다. 이 물리적 현상을 기반으로 그들은 4kW의 전력과 가변 인덕턴스를 갖춘 최초의 파라메트릭 AC 발전기를 제작했습니다.

발전기 설계에서 7 쌍의 플랫 코일이 프레임의 양쪽에 위치했으며 그 캐비티에는 돌출부가있는 강자성 디스크가 회전했습니다. 디스크가 모터에 의해 회전하도록 구동될 때 디스크의 돌출부가 각 코일 쌍 사이의 공간 안팎으로 주기적으로 이동하여 인덕턴스와 여기 진동을 변경합니다.