전기 공학 및 전자 공학의 진동 과정, 진동 유형
진동 프로세스 — 다양한 정도의 반복성을 갖는 프로세스. 모든 진동 프로세스는 주기적인 것과 비주기적인 두 가지 클래스로 나뉩니다. 이론상으로는 거의 주기적인 진동인 중간 등급도 사용합니다.
진동 과정을 주기적이라고 하며, 이 과정을 특징짓는 값은 일정 기간 T가 동일한 값을 가지면 언제든지 취해집니다.
진동 과정의 수학적 표현인 함수 f(t)는 조건 f(t + T) = f(t)를 만족하는 경우 주기 T를 갖는 주기적이라고 합니다.
주기적 진동 과정의 부류 중 주요 역할은 사인 또는 코사인의 법칙에 따라 시간에 따른 물리량의 변화가 발생하는 고조파 또는 정현파 진동에 의해 수행됩니다. 그들의 전체 기록은 다음과 같습니다.
y = f(t) = aCos((2π / T) t — φ),
여기서 a — 진동의 진폭, φ는 진동의 위상, 1/T = f — 주파수 및 2πf = ω — 주기적 또는 원형 진동의 주파수입니다.
정현파 진동의 적용 및 특성:
주기적 진동의 판독값에 해당하는 거의 주기적인 함수는 다음 조건으로 정의됩니다.
| 에프 · (t + τ) — 에프 (티) | <= ε 여기서 ε — 각 값 T에 값을 할당합니다.
이 경우의 양 τ를 거의 주기라고 합니다. 값 ε이 시간 T에서 f(t)의 평균값에 비해 매우 작으면 준주기 함수는 주기적 함수에 가까워집니다.
비주기적 진동은 주기적 진동보다 훨씬 다양합니다. 그러나 대부분의 경우 자동화에서 감쇠 또는 증가하는 정현파 진동을 충족해야 합니다.
감쇠 정현파 법칙에 따른 진동 또는 감쇠 조화 진동이라고도 하는 진동은 다음과 같은 일반적인 형식으로 나타낼 수 있습니다.
x = Ae-δTcos·(ω + φ),
여기서 t는 시간이고 A와 φ는 임의의 상수입니다. 고조파 진동 증가 법칙의 일반적인 표기법은 감쇠 계수 δ[1초]의 부호만 다릅니다.
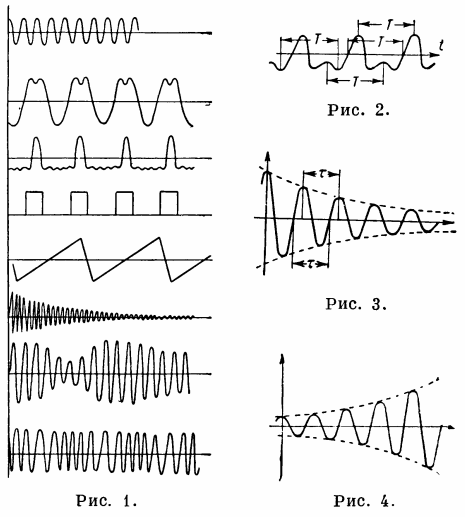
무화과. 1 — 진동 과정, Fig. 2. — 주기적 프로세스, 그림. 3. - 고조파 진동 감소, 그림. 4. - 고조파 진동의 증가.
진동 프로세스의 적용 예는 가장 간단한 진동 회로입니다.
발진기 회로(전기 회로) — 회로 자체의 매개변수에 의해 결정되는 주파수로 전기 발진이 발생할 수 있는 수동 전기 회로.
가장 간단한 발진 회로는 커패시턴스 C와 인덕턴스 L로 구성됩니다. 외부 영향이 없는 경우 주파수 εО = 1/2π√LC의 진동 감쇠.
진동의 진폭은 eg-δT로 감소합니다. 여기서 δ는 감쇠 계수입니다. δ> = eO이면 회로의 감쇠 진동이 비주기적이 됩니다.
전자 제품에서 진동 회로의 품질은 품질 계수에 의해 결정됩니다. Q = nf/δ... 진동 회로에 외부 주기적인 힘이 작용하면 강제 진동이 발생합니다. 강제 진동의 진폭은 외부 영향의 주파수가 eo(공진)에 가까운 경우 높은 Q 회로에서 크게 증가합니다. 발진 회로는 공진 증폭기의 주요 부품 중 하나이며, 발전기 및 기타 전자 장치.
이 주제에 대해서도 다음을 참조하십시오. 전압 공진 및 전류 공진 적용
