동기 전동기의 특성 및 시동 특성
동기 모터의 기계적 특성은 수평 직선의 형태를 갖습니다. 즉, 회전 속도가 부하에 의존하지 않습니다 (그림 1, a). 부하가 증가함에 따라 각도 θ가 증가합니다. 즉, 네트워크 전압 Uc의 벡터와 고정자 권선 EMF의 EMF 사이의 각도입니다(그림 1, b).
벡터 다이어그램에서 전자기 모멘트 공식을 도출할 수 있습니다.
M = (m1/ω1)(U1E0 / x1) sinθ,
여기서 m1 - 고정자 위상 수 ω1 - 고정자 필드의 각속도 U1 - 고정자 전압; E0 - 고정자 권선에 유도된 EMF NS1 - 고정자 권선의 유도 저항 θ - 고정자와 회 전자의 자화력 벡터 사이의 각도. 이 공식에서 정현파 법칙에 따라 하중에 따라 모멘트가 변한다는 것을 알 수 있습니다(그림 1, c).
무부하 각도 θ = 0, 즉 전압과 기전력은 동상입니다. 이것은 고정자 필드와 회전자 필드가 방향이 일치한다는 것을 의미합니다. 즉, 이들 사이의 공간 각도는 0입니다.
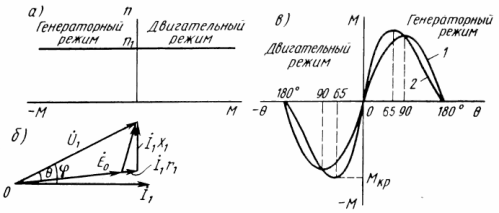
쌀. 1.동기 모터의 특성(a, b) 및 벡터 다이어그램(6): I — 고정자 전류; r1 - 고정자 권선의 능동 저항 x1 — 누설 전류 및 전기자 전류에 의해 생성된 유도 저항
부하가 증가함에 따라 토크가 증가하고 θ = 80°(곡선 1)에서 임계 최대값에 도달하며 모터는 주어진 그리드 전압 및 계자 전류에서 생성할 수 있습니다.
일반적으로 공칭 각도 θ숫자(25 ≈ 30) °는 임계값보다 3배 낮으므로 모터의 과부하 용량은 Mmax / Mnom = 1.5 + 3입니다. 로터와 더 작은 것 - 뚜렷한 것. 두 번째 경우 특성(곡선 2)은 θ = 65°에서 임계 모멘트를 가지며 이는 반응 토크의 영향으로 인해 발생합니다.
주전원 전압을 과부하하거나 감소시킬 때 모터를 동기화하지 않으려면 일시적으로 여기 전류를 증가시킬 수 있습니다. 즉, 강제 모드를 사용할 수 있습니다.
균일한 회전으로 시작 권선은 모터 작동에 영향을 미치지 않습니다. 하중이 변경되면 각도 θ가 변경되고 속도가 증가하거나 감소합니다. 그런 다음 시동 권선이 안정화 역할을 하기 시작합니다. 발생하는 비동기식 토크는 로터 속도의 변동을 완화합니다.
동기 모터는 다음과 같은 초기 특성을 특징으로 합니다.
- Az* n = AzNS //Aznom — 기동 초기 순간에 고정자를 통해 흐르는 기동 전류의 배수;
- M * n = Mn / Mnom - 시동 코일의 막대 수와 활성 저항에 따라 달라지는 시동 토크의 배수.
- M * in = MVh / Mnom — 모터가 슬립 s = 0.05에서 동기화되기 전에 비동기 모드에서 모터에 의해 생성된 입력 토크 세트;
- M * max = Mmax / Mnoy - 모터의 동기 모드에서 최대 토크 세트.
- U* n = Un • 100 /U1 — 시작 시 허용 가능한 최저 고정자 전압, %.
동기식 전기 드라이브는 예를 들어 팬, 펌프, 압축기와 같이 빈번한 시동 및 속도 제어가 필요하지 않은 설비에 사용됩니다. 동기식 전동기는 비동기식 전동기보다 효율이 높으며 과여자 상태에서 작동할 수 있습니다. 음의 각도 φ, 따라서 보상 유도 전력 다른 사용자.
동기식 모터는 설계가 더 복잡하고 직류 전원이 필요하며 슬립 링이 있지만 특히 강력한 메커니즘을 구동하는 경우 유도 모터보다 비용 효율적인 것으로 밝혀졌습니다.