전력선의 저항, 컨덕턴스 및 등가 회로
 전력선은 길이에 따라 능동 및 유도 저항과 능동 및 용량 컨덕턴스가 고르게 분포되어 있습니다.
전력선은 길이에 따라 능동 및 유도 저항과 능동 및 용량 컨덕턴스가 고르게 분포되어 있습니다.
전력 전송 네트워크의 실제 전기 계산에서 균일하게 분포된 DC 라인을 활성 r 및 유도성 x 저항과 활성 g 및 용량성 b 전도도 조합의 상수로 대체하는 것이 일반적입니다. 이 조건에 해당하는 U자형 선로의 등가 회로는 그림 1과 같습니다. 1, 아.
전압이 35kV이고 전도율 g 및 b 미만인 로컬 전력 전송 네트워크를 계산할 때 직렬 연결된 능동 및 유도 저항으로 구성된 더 간단한 등가 회로를 무시하고 사용할 수 있습니다(그림 1, b).
선형 저항은 공식에 의해 결정됩니다.
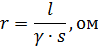
여기서 l은 와이어의 길이, m입니다. s는 와이어 또는 케이블 코어의 단면, mmg γ는 재료의 특정 설계 전도도, m / ohm-mm2입니다.
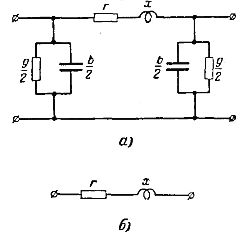
쌀. 1. 회선 교체 계획: a - 지역 송전망용; b - 로컬 전력 전송 네트워크용.
단일 코어 및 다중 코어 와이어의 20 ° C 온도에서 계산 된 비 전도도의 평균 계산 값은 실제 단면적과 다중 코어 와이어를 비틀 때 길이 증가를 고려하여 53m / 옴입니다. ∙ 구리의 경우 mm2, 알루미늄의 경우 32m/ohm ∙ mm2.
강선의 활성 저항은 일정하지 않습니다. 와이어를 통과하는 전류가 증가함에 따라 표면 효과가 증가하므로 와이어의 활성 저항이 증가합니다. 강선의 활성 저항은 흐르는 전류 값에 따라 실험 곡선 또는 표에 의해 결정됩니다.
라인 유도 저항. 전선의 재배치 (전위)로 3 상 전류선을 만들면 주파수 50Hz에서 선 길이 1km의 위상 유도 저항은 다음 공식으로 결정할 수 있습니다
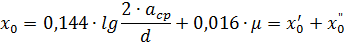
여기서: asr은 와이어 축 사이의 기하 평균 거리입니다.
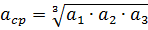
a1, a2 및 a3은 서로 다른 위상의 도체 축 사이의 거리이고 d는 도체에 대한 GOST 표에 따라 취해진 도체의 외경입니다. μ는 금속 도체의 상대 자기 투자율입니다. 비철금속 와이어의 경우 μ = 1; x'0 - 도체 외부의 자속으로 인한 선로의 외부 유도 저항; x «0 - 도체 내부에서 닫힌 자속으로 인한 라인의 내부 유도 저항.
라인 길이 l km 당 유도 저항
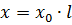
비철금속 도체가 있는 가공선의 유도 저항 x0은 평균 0.33-0.42ohms/km입니다.
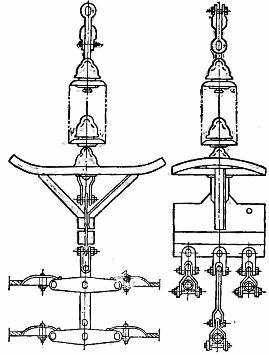
코로나 손실을 줄이기 위해 330-500kV의 전압을 사용하는 라인(아래 참조)은 직경이 큰 하나의 코어가 아니라 서로 짧은 거리에 위치한 상당 2개 또는 3개의 강철-알루미늄 도체로 수행됩니다. 이 경우 라인의 유도 저항이 크게 감소합니다. 무화과에서. 그림 2는 500kV 라인에서 위상의 유사한 구현을 보여 주며 3개의 도체가 측면이 40cm인 정삼각형의 꼭지점에 위치하며 위상 도체는 섹션에 여러 개의 단단한 줄무늬로 고정됩니다.
상당 여러 개의 전선을 사용하는 것은 전선의 직경을 늘리는 것과 같으며, 이는 전선의 유도 저항을 감소시킵니다. 후자는 두 번째 공식을 사용하여 계산할 수 있습니다. 오른쪽의 두 번째 항을 n으로 나누고 와이어의 외경 d 대신 공식에 의해 결정되는 등가 직경 de를 대체합니다.
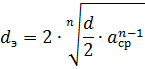
여기서 n - 라인의 한 위상에 있는 도체의 수 acp — 한 상의 도체 사이의 기하 평균 거리.
위상당 2개의 와이어를 사용하면 라인의 유도 저항이 약 15-20% 감소하고 3개 와이어를 사용하면 25-30% 감소합니다.
위상 도체의 총 단면적은 필요한 설계 단면적과 동일하며 후자는 어쨌든 2개 또는 3개의 도체로 분할되므로 이러한 라인을 일반적으로 분할 도체 라인이라고 합니다.
강선은 훨씬 더 큰 x0 값을 갖습니다. 투자율 1 이상이 되고 두 번째 공식의 두 번째 용어가 결정적입니다. 즉, 내부 유도 저항 x «0입니다.
쌀. 2. 화환을 거는 500 평방 미터 단상 3 분할 와이어.
와이어를 통해 흐르는 전류 값에 대한 강철의 자기 투자율의 의존성으로 인해 강철 와이어에서 x «0을 결정하는 것은 매우 어렵습니다. 따라서 실제 계산에서 강선의 x» 0은 실험적으로 얻은 곡선 또는 표에서 결정됩니다.
3코어 케이블의 유도 저항은 다음 평균값을 기반으로 할 수 있습니다.
• 3선 케이블의 경우 35kV — 0.12ohms/km
• 3-10kv-0.07-0.03ohms/km의 3선 케이블용
• 최대 1kV-0.06-0.07ohms/km의 3선 케이블용
능동 전도선은 유전체의 유효 전력 손실로 정의됩니다.
모든 전압의 가공선에서는 공기 오염이 심한 지역에서도 절연체를 통한 손실이 적기 때문에 고려하지 않습니다.
전압이 110kV 이상인 가공선에서 특정 조건에서 전선을 둘러싼 공기의 강렬한 이온화로 인해 전선에 코로나가 나타나고 보라색 빛과 특징적인 딱딱 거리는 소리가 동반됩니다. 와이어 크라운은 습한 날씨에 특히 강렬합니다. 코로나에 대한 전력 손실을 줄이는 가장 근본적인 방법은 도체의 직경을 늘리는 것입니다. 왜냐하면 후자가 증가함에 따라 전기장의 강도가 증가하여 도체 근처의 공기 이온화가 감소하기 때문입니다.
110kV 라인의 경우 코로나 조건에서 도체의 직경은 최소 10-11mm(도체 AC-50 및 M-70), 154kV 라인의 경우 최소 14mm(도체 AC-95)여야 합니다. 220kV 라인의 경우 - 22mm 이상(도체 AC -240).
지정되고 큰 도체 직경의 110-220kV 가공선 도체에서 코로나의 유효 전력 손실은 중요하지 않으므로(선 길이 1km당 수십 킬로와트) 계산에서 고려되지 않습니다.
330 및 500kV 라인에서는 위상당 2개 또는 3개의 도체가 사용되며, 이는 앞서 언급한 바와 같이 도체 직경의 증가와 동일하므로 도체 근처의 전계 강도가 크게 증가합니다. 줄어들고 전도체가 약간 부식되었습니다.
35kV 이하의 케이블 라인에서 유전체의 전력 손실은 적고 고려되지 않습니다. 전압이 110kV 이상인 케이블 라인에서 유전 손실은 길이 1km당 수 킬로와트에 이릅니다.
컨덕터 사이 및 컨덕터와 접지 사이의 커패시턴스로 인한 라인의 용량성 전도.
실제 계산에 충분한 정확도로 3상 가공선의 용량성 컨덕턴스는 공식에 의해 결정될 수 있습니다.
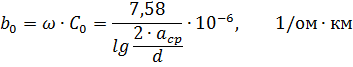
여기서 C0은 라인의 작업 용량입니다. ω - 교류의 각 주파수; acp 및 d — 위를 참조하십시오.
이 경우 지반의 전도도와 지반으로 되돌아오는 전류의 깊이는 고려하지 않고 선로를 따라 도체를 재배치하는 것으로 가정한다.
케이블의 경우 작업 용량은 공장 데이터에 따라 결정됩니다.
선형 전도도 l km
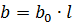
라인에 커패시턴스가 존재하면 용량성 전류가 흐르게 됩니다. 용량성 전류는 해당 위상 전압보다 90° 앞서 있습니다.
일정한 용량성 전류가 길이를 따라 균일하게 분포된 실제 라인에서 용량성 전류는 라인 전체의 전압이 크기가 일정하지 않기 때문에 라인의 길이를 따라 균일하지 않습니다.
DC 전압을 수용하는 라인 시작 부분의 용량성 전류
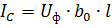
여기서 Uph는 선상 전압입니다.
Capacitive line power(선로에서 발생하는 전력)
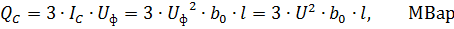
여기서 U는 상간 전압, sq.
세 번째 공식에서 라인의 용량 성 전도도는 도체 사이의 거리와 도체의 직경에 거의 의존하지 않습니다. 라인에서 생성되는 전력은 라인 전압에 크게 의존합니다. 가공선 35kV 이하의 경우 매우 작습니다. 길이가 100km인 110kV 라인의 경우 Qc≈3 Mvar. 길이가 100km인 220kV 라인의 경우 Qc≈13Mvar. 분할 와이어를 사용하면 라인 용량이 증가합니다.
케이블 네트워크의 용량성 전류는 20kV 이상의 전압에서만 고려됩니다.