전자석의 견인력

전자석이 강자성체를 끌어당기는 힘은 자속 F 또는 동등하게 유도 B와 전자석 S의 단면적에 따라 달라집니다.

전자석의 압력은 공식에 의해 결정됩니다.

F = 40550 ∙ B ^ 2 ∙ S,

여기서 F는 전자석의 압력, kg(힘은 뉴턴 단위로도 측정, 1kg = 9.81N 또는 1N = 0.102kg)입니다. B — 유도, T; S는 전자석의 단면적 m2입니다.

의 예

1. 수도꼭지 전자석은 자기 회로입니다(그림 1). 자기 유도가 B = 1 T이고 전자석 각 극의 단면적이 S = 0.02 m2 인 경우 말굽 기중기 전자석의 양력은 얼마입니까 (그림 1, b)? 전자석과 전기자 사이의 간격 효과를 무시하십시오.

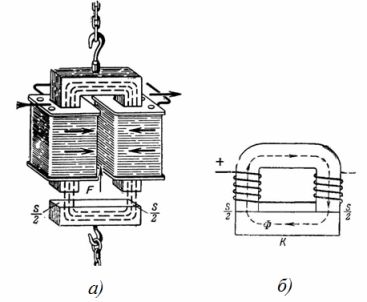
쌀. 1. 리프팅 전자석

F = 40550 ∙ B ^ 2 ∙ S; F = 40550 ∙ 1^2 ∙ 2 ∙ 0.02 = 1622kg.

2. 원형 강철 전자석은 그림에 표시된 치수를 갖습니다. 2, 가 및 나. 전자석의 양력은 3T입니다. 전자석 코어의 단면적 n을 결정하십시오. p. 및 자화 전류 I = 0.5A에서 코일의 권선 수.

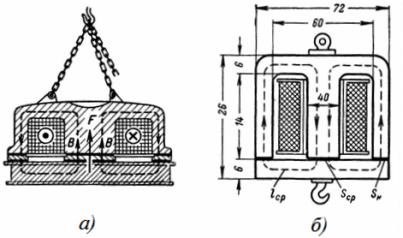
쌀. 2. 원형 전자석

자속은 원형 내부 코어를 통과하고 원통형 몸체를 통해 되돌아옵니다. 코어 Sc와 케이싱 Sk의 단면적은 거의 동일하므로 코어와 케이싱의 유도 값은 거의 동일합니다.

Sc = (π ∙ 40^2) / 4 = (3.14 ∙ 1600) / 4 = 1256 cm2 = 0.1256 m2,

Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3.14 / 4 ∙ (5184-3600) = 1243.5 cm2 = 0.12435 m2;

S = Sc + Sk = 0.24995m2 ≈0.25m2.

전자석에서 필요한 유도는 공식 F = 40550 ∙ B ^ 2 ∙ S에 의해 결정됩니다.

여기서 B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0.25)) = 0.5475 T.

이 유도 전압은 주강의 자화 곡선에서 찾을 수 있습니다.

H = 180A / m.

필드 라인의 평균 길이(그림 2, b) lav = 2 ∙ (20 + 23) = 86 cm = 0.86 m.

자화력 I ∙ ω = H ∙ lav = 180 ∙ 0.86 = 154.8 Av; 나는 = (나는 ∙ ω) / 나는 = 154.8 / 0.5 = 310A.

실제로 n. s, 즉 전류와 권수는 전자석과 전기자 사이에 불가피한 에어 갭이 있어 자기 회로의 자기 저항을 크게 증가시키기 때문에 몇 배 더 커야 합니다. 따라서 전자석을 계산할 때 에어 갭을 고려해야 합니다.

3. 수도꼭지 용 전자석 코일은 1350 회 감고 전류 I = 12A가 흐르고 전자석의 치수는 그림에 나와 있습니다. 3. 전기자에서 1cm 떨어진 거리에서 전자석이 들어 올리는 무게는 얼마이며 중력 후에는 얼마를 견딜 수 있습니까?

쌀. 3. 전자기 코일

I ∙ ω가 있는 N.의 대부분은 에어 갭을 통해 자속을 전도하는 데 사용됩니다. I ∙ ω≈Hδ ∙ 2 ∙ δ.

자화력 I ∙ ω = 12 ∙ 1350 = 16200 A.

H ∙ δ = 8 ∙ 10 ^ 5 ∙ B이므로 Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0.02입니다.

따라서 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0.02, 즉 B = 1.012T.

n의 일부이므로 귀납은 B = 1 T라고 가정합니다. c.I ∙ ω는 강철에서 자속 전도에 사용됩니다.

이 계산을 공식 I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс로 확인해 봅시다.

자력선의 평균 길이는 lav = 2 ∙ (7 + 15) = 44 cm = 0.44 m입니다.

B = 1T(10000Gs)에서의 강도 Hc는 자화 곡선에서 결정됩니다.

Hc = 260A/m I ∙ ω = 0.8 ∙ B ∙ 2 + 2.6 ∙ 44 = 1.6 ∙ 10000 + 114.4 = 16114 Av.

자화력 I ∙ ω = 16114 Av 유도를 생성 B = 1 T는 사실상 주어진 n과 같습니다. v. I ∙ ω = 16200 Av.

코어와 콘의 총 단면적은 S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0.006m2입니다.

전자석은 1cm 거리에서 F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0.006 = 243.3 kg의 전하를 끌어당깁니다.

전기자를 끌어당긴 후에 에어 갭이 실질적으로 사라지기 때문에 전자석은 훨씬 더 큰 하중을 견딜 수 있습니다. 이 경우 전체 n. c.I ∙ ω는 강철에서만 자속 전도에 사용되므로 I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368A/cm = 36800A/m.

이러한 전압에서 강철은 실질적으로 포화되고 유도는 약 2T입니다. 전자석은 F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0.006 = 973 kg의 힘으로 전기자를 끌어당깁니다.

4. 신호(깜박임) 릴레이는 둥근 코어가 있는 외장형 전자석 1과 전자석에 전류를 공급한 후 신호 숫자를 여는 깜박이 3을 끌어 당기고 해제하는 밸브형 전기자 2로 구성됩니다(그림 1). 4).

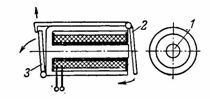
쌀. 4. 갑옷 전자석

자화 강도는 I ∙ ω = 120 Av, 공극은 δ = 0.1cm, 전자석의 총 단면적은 S = 2cm2입니다. 릴레이의 당기는 힘을 추정합니다.

인덕턴스 B는 방정식 I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ를 사용하여 연속적인 근사치로 결정됩니다.

n하자. c. Hc ∙ lc는 15% I ∙ ω, 즉 18 Av.

그런 다음 I ∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = Hδ ∙ 0.2; Hδ = 102/0.2 = 510A/cm = 51000A/m.

따라서 귀납법 B를 찾습니다.

Hδ = 8 ∙ 10^5 V; B = Hδ / (8 ∙ 10^5) = 51000 / (8 ∙ 10 ^ 5) = 0.0637 T.

공식 F = 40550 ∙ B ^ 2 ∙ S에서 값 B를 대입하면 다음을 얻습니다.

F = 40550 ∙ 0.0637^2 ∙ 0.0002 = 0.0326kg.

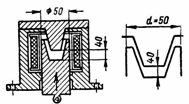
5. DC 제동 솔레노이드(그림 5)에는 테이퍼 스톱이 있는 피스톤 전기자가 있습니다. 전기자와 코어 사이의 거리는 4cm이고 작업 직경(원형 접촉 영역이 있는 코어) d = 50mm입니다. 전기자는 50kg의 힘으로 코일 안으로 당겨집니다. 중간 힘선의 길이 lav = 40cm n을 결정하십시오. pp. 및 코일 전류가 3000회인 경우.

쌀. 5. DC 브레이크 솔레노이드

전자석의 작업 영역의 면적은 직경 d = 5cm 인 원의 면적과 같습니다.

S = (π ∙ d ^ 2) / 4 = 3.14 / 4 ∙ 25 = 19.6 cm2.

힘 F = 50kg을 생성하는 데 필요한 유도 B는 방정식 F = 40550 ∙ B ^ 2 ∙ S에서 구합니다.

여기서 B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0.00196)) = 0.795 T.

자화력 I ∙ ω = Hс ∙ lс + Hδ ∙ δ.

강철 Hc ∙ lc의 자화 강도는 15% I ∙ ω라는 사실을 기반으로 단순화된 방식으로 결정됩니다.

나는 ∙ ω = 0.15 ∙ 나는 ∙ ω + Hδ ∙ δ; 0.85 ∙ I ∙ ω = Hδ ∙ δ; 0.85 ∙ 나는 ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; 나는 ∙ ω = (8 ∙ 10 ^ 5 ∙ 0.795 ∙ 0.04) / 0.85 = 30,000 Av.

자화 전류 I = (I ∙ ω) / ω = 30000/3000 = 10A.