인덕턴스 계산 방법

역학적으로 질량이 있는 물체가 공간 가속에 저항하여 관성을 나타내는 것처럼 인덕턴스는 도체의 전류가 변경되는 것을 방지하여 자기 유도 EMF를 나타냅니다. 이것은 자기 유도의 EMF로, 유지하려는 전류 감소와 감소시키려는 전류 증가에 반대합니다.

사실 회로의 전류를 변경(증가 또는 감소)하는 과정에서 이 전류에 의해 생성된 자속도 변경되며, 이는 주로 이 회로에 의해 제한된 영역에 국한됩니다. 그리고 자속이 증가하거나 감소함에 따라 동일한 회로에서 자체 유도의 EMF를 유도합니다(Lenz의 규칙에 따라 — 발생 원인, 즉 처음에 언급한 전류에 대해). 여기서 인덕턴스 L은 전류 I와 총 자속 Φ 사이의 비례 계수라고 하며, 이 전류는 다음과 같이 생성됩니다.

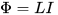
따라서 회로의 인덕턴스가 높을수록 결과적인 자기장보다 강하고 전류가 변경되는 것을 방지하므로(전류를 생성하는 필드) 더 큰 인덕턴스를 통해 전류가 변경되는 데 시간이 더 오래 걸리며, 동일한 인가 전압으로. 다음 진술도 참입니다. 인덕턴스가 높을수록 회로를 통과하는 자속이 변할 때 회로 양단의 전압이 커집니다.

일정한 속도로 특정 영역의 자속을 변경한 다음 이 영역을 다른 회로로 덮음으로써 인덕턴스가 더 큰 회로에서 더 많은 전압을 얻을 수 있습니다(변압기, Rumkorf 코일 등이 이 원리에 따라 작동함).

그러나 루프 인덕턴스는 어떻게 계산됩니까? 전류와 자속 사이의 비례 계수를 찾는 방법은 무엇입니까? 가장 먼저 기억해야 할 것은 헨리(H)에서 인덕턴스가 변한다는 것입니다. 인덕턴스가 1헨리인 회로의 단자에서 전류가 초당 1암페어씩 변하면 1볼트의 전압이 나타납니다.

인덕턴스의 크기는 회로의 기하학적 치수(길이, 너비, 회전 수 등)와 매체의 자기 특성(예를 들어 내부에 페라이트 코어가 있는 경우)의 두 가지 매개변수에 따라 달라집니다. 코일 내부에 코어가 없는 경우보다 인덕턴스가 더 큽니다).

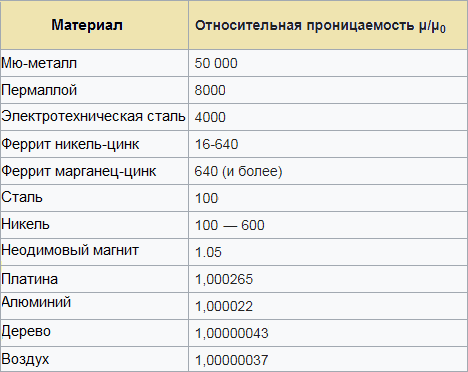
생성된 인덕턴스를 계산하려면 코일 자체의 모양과 그 내부의 매체가 어떤 투자율을 가질지 알아야 합니다(매체의 상대 투자율은 진공의 투자율과 자기 주어진 매체의 투과성.물론 재료에 따라 다릅니다.) …

가장 일반적인 형태의 코일(원통형 솔레노이드, 토로이드 및 긴 와이어)의 인덕턴스 계산 공식을 살펴보겠습니다.

인덕턴스를 계산하는 공식은 다음과 같습니다. 솔레노이드 - 길이가 직경보다 훨씬 큰 코일:

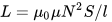
보시다시피 권선 수 N, 권선 길이 l 및 코일 S의 단면적을 알면 코어가 없거나 코어가있는 코일의 대략적인 인덕턴스를 찾을 수 있습니다. 진공의 투과성은 일정한 값입니다.

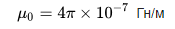
토로이드 코일의 인덕턴스, 여기서 h는 토로이드의 높이, r은 토로이드의 내경, R은 토로이드의 외경:

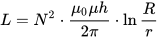
얇은 와이어의 인덕턴스(단면의 반경은 길이보다 훨씬 작음), 여기서 l은 와이어의 길이이고 r은 단면의 반경입니다. 지수 i와 e를 갖는 Mu는 내부(내부, 도체 재료) 및 외부(외부, 도체 외부 재료) 환경의 상대 투자율:

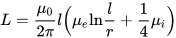
상대 유전율 표는 특정 자성 재료를 코어로 사용하는 회로(와이어, 코일)에서 기대할 수 있는 인덕턴스를 추정하는 데 도움이 됩니다.