인덕턴스란?
인덕턴스는 자기장의 에너지가 저장되는 전기 회로의 이상화된 요소라고 합니다. 전기장 에너지의 저장 또는 전기 에너지를 다른 유형의 에너지로 변환하지 않습니다.
이상적인 요소인 인덕턴스에 가장 가까운 것은 전기 회로의 실제 요소입니다. 유도 코일.
인덕턴스와 달리 인덕턴스 코일은 전기장의 에너지를 저장하고 전기 에너지를 다른 유형의 에너지, 특히 열로 변환합니다.
정량적으로, 자기장의 에너지를 저장하는 전기 회로의 실제 및 이상화 요소의 능력은 인덕턴스라는 매개변수로 특징지어집니다.
따라서 "인덕턴스"라는 용어는 전기 회로의 이상화된 요소의 이름, 이 요소의 특성을 정량적으로 특성화하는 매개 변수의 이름 및 유도 코일의 주요 매개 변수의 이름으로 사용됩니다.
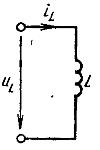
쌀. 1. 인덕턴스의 기존 그래픽 표기법
유도 코일의 전압과 전류 사이의 관계가 결정됩니다. 전자기 유도의 법칙, 유도 코일을 관통하는 자속이 변할 때 코일 ψ의 자속 쇄교의 변화율에 비례하여 기전력 e가 유도되고 전류가 그것은 자속의 변화를 방지하는 경향이 있습니다.
e = — dψ / dt
코일의 자속 연결은 개별 권선을 관통하는 자속의 대수 합과 같습니다.
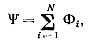
여기서 N은 코일 회전 수입니다.
일반적으로 코일의 각 권선을 관통하는 자속 F는 두 가지 구성 요소를 포함할 수 있습니다. 자기 유도에 대한 자속 Fsi 및 외부 필드의 자속 Fvp: F — Fsi + Fvp.
첫 번째 구성 요소는 코일을 통해 흐르는 전류로 인해 발생하는 자속이고, 두 번째 구성 요소는 코일의 전류와 관련이 없는 자기장에 의해 결정됩니다. 즉, 지구의 자기장, 다른 코일의 자기장 및 영구 자석… 자속의 두 번째 구성 요소가 다른 코일의 자기장에 의해 발생하는 경우 상호 유도 자속이라고 합니다.
코일 자속 ψ 및 자속 Φ는 자기 유도 자속 쇄교 ψsi 및 외부 필드 자속 쇄교 ψvp의 두 구성 요소의 합으로 나타낼 수 있습니다.
ψ= ψsi + ψvp
e = esi + dvp,
여기서 eu는 자기 유도의 EMF이고 evp는 외부 필드의 EMF입니다.
유도 코일 외부 필드의 자기 플럭스가 0이고 자기 유도 플럭스만 코일을 통과하면 자기 유도의 EMF.
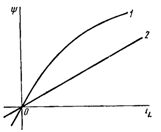
인덕턴스 플럭스 관계는 코일을 통해 흐르는 전류에 따라 달라집니다. 유도 코일의 암페어 특성인 Weber라고 하는 이 종속성은 일반적으로 비선형 특성을 가집니다(그림 2, 곡선 1).
특별한 경우, 예를 들어 자기 코어가 없는 코일의 경우 이 종속성은 선형일 수 있습니다(그림 2, 곡선 2).
쌀. 2. 유도 코일의 웨버 암페어 특성: 1 — 비선형, 2 — 선형.
SI 단위에서 인덕턴스는 헨리(H)로 표시됩니다.
회로를 분석할 때 코일에 유도된 EMF 값은 일반적으로 고려되지 않지만 단자의 전압은 양의 방향이 전류의 양의 방향과 일치하도록 선택됩니다.
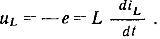
전기 회로의 이상적인 요소인 인덕턴스는 자기장의 에너지를 저장하는 코일의 능력을 반영하는 유도 코일의 단순화된 모델로 볼 수 있습니다.
선형 인덕턴스의 경우 단자 양단의 전압은 전류 변화율에 비례합니다. 직류가 인덕턴스를 통해 흐를 때 단자 양단의 전압은 0이므로 직류에 대한 인덕턴스의 저항은 0입니다.