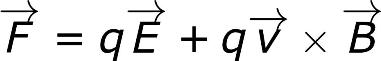전자기장 강도
전자기장에 대해 이야기할 때 일반적으로 전류의 자기장, 실제로는 움직이는 전하 또는 전파의 자기장을 의미합니다. 실제로 전자기장은 고려 중인 공간 영역에 존재하게 되는 힘의 결과 필드입니다. 전기장과 자기장.
전자기장의 각 구성 요소(전기 및 자기)는 서로 다른 방식으로 전하에 영향을 미칩니다. 전기장은 정지 전하와 이동 전하 모두에 작용하는 반면 자기장은 이동 전하(전류)에만 작용합니다.
사실, 자기 상호작용 동안 자기장 상호작용(예를 들어 소스는 지정되지 않았지만 유도가 알려진 외부 자기장과 움직이는 전하에 의해 생성된 자기장)과 전기적 상호작용 중에 상호작용한다는 것을 이해하기 쉽습니다. 전기장 상호 작용 - 소스가 지정되지 않은 외부 전기장과 해당 전하의 전기장.
수학적 장치를 사용하여 힘을 찾는 편의를 위해, 고전 물리학에서, 전기장 세기 E와 자기장 유도 B의 개념, 뿐만 아니라 자기장의 유도 및 자기 매질의 특성과 관련하여 보조량, 자기장 강도 H… 이러한 벡터 물리량을 개별적으로 고려하고 동시에 물리적 의미를 이해하십시오.

전계 강도 E
공간의 특정 지점에 전기장이 존재하면 전기장의 세기 E와 전하 q의 크기에 비례하는 힘 F가 이 필드 측면의 해당 지점에 배치된 전하에 작용합니다. 외부 전기장의 소스 매개변수를 알 수 없는 경우 q와 F를 알면 소스가 누구인지 생각하지 않고도 공간의 주어진 지점에서 전기장 강도 벡터 E의 크기와 방향을 찾을 수 있습니다. 이 전기장.
전기장이 일정하고 균일하면 전하에 대한 측면의 힘의 작용 방향은 전기장에 대한 전하의 이동 속도 및 방향에 의존하지 않으므로 관계없이 변경되지 않습니다. 요금이 고정되어 있는지 이동하는지 여부. 전계 강도 NE에서 V / m(미터당 볼트) 단위로 측정됩니다.
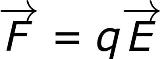
자기장 유도 B
공간의 특정 지점에 자기장이 존재하는 경우 해당 필드 측면의 해당 지점에 배치된 정지 전하에는 아무런 작용도 하지 않습니다.
전하 q가 움직이면 힘 F가 자기장 측면에서 발생하고 전하 q의 크기와 이 필드에 대한 운동의 방향과 속도 v 모두에 따라 달라집니다. 주어진 자기장의 자기장 벡터 유도 B의 크기와 방향.
따라서 자기장 소스의 매개 변수를 모르는 경우 힘 F, 전하의 크기 q 및 속도 v, 주어진 필드 지점에서 자기 유도 벡터 B의 크기 및 방향을 알 수 있습니다. 설립하다.
따라서 자기장이 일정하고 균일하더라도 측면의 힘의 작용 방향은 자기장에 대한 전하의 속도와 이동 방향에 따라 달라집니다. SI 시스템의 자기장 유도는 T(Tesla) 단위로 측정됩니다.
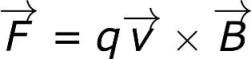
자기장의 세기 H
전하, 즉 전류를 이동시키면 자기장이 발생하는 것으로 알려져 있다. 자기장 유도는 전류와 관련이 있습니다. 프로세스가 진공에서 발생하는 경우 공간에서 선택한 지점에 대한 이 관계는 진공의 자기 투자율로 표현될 수 있습니다.
관계에 대한 더 나은 이해를 위해 자기 유도 B와 자기장 H의 강도는 다음 예를 고려하십시오. 코어가 없는 전류 I가 있는 코일 중심에서의 자기 유도는 동일한 전류 I가 있는 동일한 코일 중심에서의 자기 유도와 다를 것입니다. 강자성 코어가 배치되어 있습니다.
코어가 있는 경우와 없는 경우(동일한 자기장 강도 H에서) 자기 유도의 양적 차이는 도입된 코어 재료와 진공의 자기 투자율 차이와 같습니다. SI 자기장은 A/m 단위로 측정됩니다.
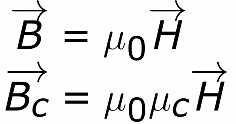
전기장과 자기장(로렌츠 힘) 및 자기장의 결합된 작용. 이 총 힘을 로렌츠 힘이라고 합니다.