진공 상태의 전류

기술적인 의미에서 공간은 진공이라고 불리며, 일반적인 기체 매체에 비해 물질의 양이 미미합니다. 진공 압력은 대기압보다 적어도 두 자릿수 낮습니다. 이러한 조건에서는 실제로 무료 전하 캐리어가 없습니다.

그러나 우리가 알고 있듯이 전기 충격 전기장의 작용 하에서 하전 입자의 정렬 된 움직임이라고하는 반면, 진공 상태에서는 정의에 따라 안정적인 전류를 형성하기에 충분한 수의 하전 입자가 없습니다. 이것은 진공 상태에서 전류를 생성하려면 어떻게든 전류에 하전 입자를 추가해야 함을 의미합니다.

1879년에 토마스 에디슨은 금속 음극(음극)을 가열하여 전자가 빠져나가기 시작하는 상태로 진공 상태에서 자유 전자를 얻는 입증된 방법 중 하나인 열전자 복사 현상을 발견했습니다. 이 현상은 많은 진공 전자 장치, 특히 진공관에서 사용됩니다.

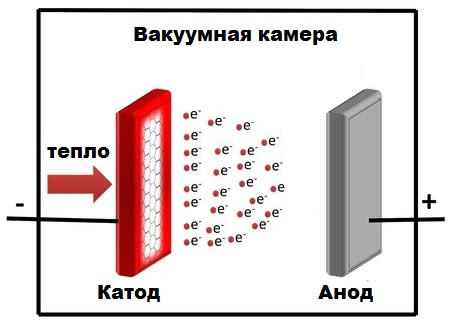
두 개의 금속 전극을 진공에 놓고 DC 전압원에 연결한 다음 음극(음극)을 가열하기 시작합니다. 이 경우 음극 내부 전자의 운동 에너지가 증가합니다. 이렇게 추가로 얻은 전자 에너지가 포텐셜 장벽을 극복하기에 충분하다면(캐소드 금속의 일함수 수행) 이러한 전자는 전극 사이의 공간으로 빠져나갈 수 있을 것입니다.

전극 사이에 있기 때문에 전기장 (위 소스에 의해 생성됨), 이 필드에 들어가는 전자는 양극(양극) 방향으로 가속되기 시작해야 합니다. 즉, 이론적으로 진공 상태에서 전류가 발생합니다.

그러나 이것이 항상 가능한 것은 아니며, 전자빔이 음극 표면의 잠재적 피트를 극복할 수 있는 경우에만 가능하며, 그 존재는 음극 근처에 공간 전하(전자 구름)가 나타나기 때문입니다.

일부 전자의 경우 전극 사이의 전압이 평균 운동 에너지에 비해 너무 낮을 것입니다. 이것은 우물을 빠져나가기에 충분하지 않고 다시 되돌아갈 것입니다. 전기장에 의해 가속되기 시작합니다. 따라서 전극에 가해지는 전압이 높을수록 더 많은 전자가 음극을 떠나 진공 상태에서 전류 캐리어가 됩니다.

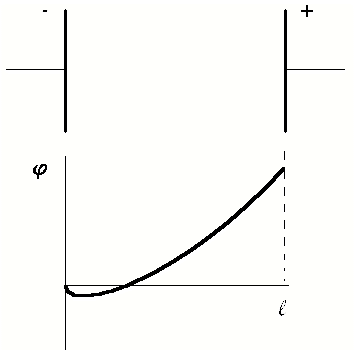
따라서 진공 상태에 있는 전극 사이의 전압이 높을수록 음극 근처의 전위 우물 깊이는 작아집니다.그 결과, 열이온 복사 동안 진공에서의 전류 밀도는 Langmuir의 법칙(미국 물리학자 Irving Langmuir를 기리기 위해) 또는 세 번째 법칙이라는 관계에 의해 양극 전압과 관련이 있음이 밝혀졌습니다.

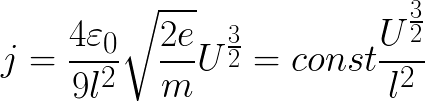
옴의 법칙과 달리 여기서 관계는 비선형입니다. 또한, 전극 사이의 전위차가 커질수록 진공 전류 밀도는 음극의 전자 구름에서 나온 모든 전자가 양극에 도달하는 조건인 포화가 발생할 때까지 증가합니다. 전극 사이의 전위차를 더 높이면 전류가 증가하지 않습니다. 아르 자형

다른 음극 물질은 다른 방사율을 가지며, 포화 전류를 특징으로 합니다.포화 전류 밀도는 Richardson-Deshman 공식에 의해 결정될 수 있으며 전류 밀도를 음극 물질의 매개 변수와 관련시킵니다.

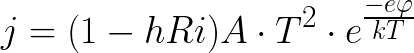
여기:

이 공식은 양자 통계를 기반으로 과학자들이 도출했습니다.