투자율(mu)이란

우리는 코일의 인덕턴스가 코일이 위치한 환경의 특성에 크게 의존한다는 것을 다년간의 기술 관행을 통해 알고 있습니다. 강자성 코어가 알려진 인덕턴스 L0의 구리선 코일에 추가되면 이전의 다른 상황에서 이 코일의 자기 유도 전류(추가 폐쇄 및 개방 전류)가 여러 번 증가할 것이며 실험은 무엇을 의미하는지 확인할 것입니다. 몇 배로 증가 인덕턴스이제 L과 같습니다.

실험 관찰

설명된 코일 내부와 주변 공간을 채우는 물질인 매체가 균질하고 도체를 통해 흐르는 전류에 의해 생성된다고 가정합니다. 자기장 국경을 넘지 않고 이 특정 지역에만 위치합니다.

코일이 닫힌 링 모양인 토로이드 모양이면 토로이드 외부에 자기장이 거의 없기 때문에 필드와 함께 이 매체는 코일의 부피에만 집중됩니다.이 위치는 모든 자력선이 축을 따라 내부에 집중되어 있는 솔레노이드인 긴 코일에도 유효합니다.

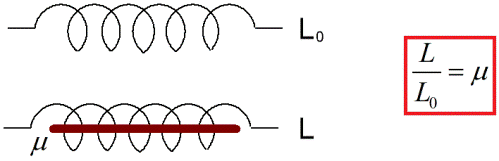
예를 들어 진공 상태에서 일부 회로 또는 코어리스 코일의 인덕턴스가 L0과 같다고 가정합니다. 그런 다음 동일한 코일에 대해 주어진 코일의 자기장 선이 존재하는 공간을 채우는 균질 물질에 이미 인덕턴스를 L로 둡니다. 이 경우 L / L0 비율은 아무것도 아님이 밝혀졌습니다. 지정된 물질의 상대 자기 투자율(때로는 "자기 투자율"이라고도 함).

자명해집니다. 자기 투자율은 주어진 물질의 자기 특성을 특징짓는 양입니다. 종종 이것은 물질의 상태(및 온도 및 압력과 같은 환경 조건) 및 특성에 따라 달라집니다.

용어 이해

자기장에 있는 물질과 관련된 «자기 투자율»이라는 용어의 도입은 전기장에 있는 물질에 대한 «유전 상수»라는 용어의 도입과 유사합니다.

상기 공식 L/L0에 의해 결정되는 자기 투자율의 값은 주어진 물질의 절대 자기 투자율과 절대 공극(진공)의 비율로 표현될 수도 있습니다.

쉽게 알 수 있습니다. 상대 자기 투자율(자기 투자율이라고도 함)은 차원이 없는 양입니다. 그러나 절대 자기 투자율은 진공의 자기 투자율(절대!)과 동일한 치수 Hn/m을 가집니다(이것은 자기 상수입니다).

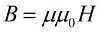
실제로 우리는 환경(자기)이 회로의 인덕턴스에 영향을 미치는 것을 볼 수 있으며, 이는 환경의 변화가 회로를 관통하는 자속 Φ의 변화로 이어지고 따라서 유도 B의 변화로 이어진다는 것을 분명히 보여줍니다. , 자기장의 각 지점에 적용됩니다.

이 관찰의 물리적 의미는 동일한 코일 전류(동일한 자기 강도 H에서)에 대해 자기장의 유도가 자기 투자율 mu를 가진 물질에서 완전 진공.

이렇게 된 이유는 매체는 자기화, 자체적으로 자기장을 갖기 시작하는데, 이렇게 자화될 수 있는 물질을 자석이라고 합니다.

절대 자기 투자율의 측정 단위는 1 H / m (미터당 헨리 또는 암페어 제곱당 뉴턴), 즉 자기장 전압 H 1 A / m에서 이러한 매체의 투자율입니다. 1의 자기유도가 일어난다 T.

현상의 물리적 그림

위에서부터 전류 루프의 자기장의 작용에 따라 다른 물질 (자석)이 자화되고 결과적으로 자기장의 합인 자기장이 얻어지는 것이 분명합니다. 즉, 자화된 매체의 자기장입니다. 더하기 전류 루프, 이것이 매체가 없는 전류 전용 필드 회로와 크기가 다른 이유입니다. 자석이 자화되는 이유는 각 원자에 가장 작은 전류가 존재하기 때문입니다.

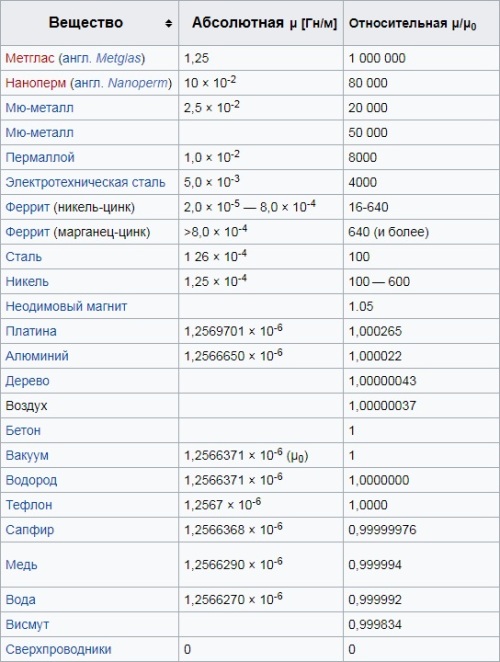
자기 투자율의 값에 따라 물질은 반자성(1 미만 - 인가된 필드에 대해 자화됨), 상자성(2개 이상 - 인가된 필드 방향으로 자화됨) 및 강자성체(1개 이상)로 분류됩니다. - 자화되고 적용된 자기장의 비활성화 후 자화됨).

강자성체는 히스테리시스따라서 순수한 형태의 "자기 투자율"의 개념은 강자성체에는 적용할 수 없지만 특정 범위의 자화에서는 대략적으로 자화 곡선의 선형 부분을 구별할 수 있으며 이를 계산할 수 있습니다. 자기 투자율.

초전도체에서 자기 투자율은 0이고(자기장은 부피에 따라 완전히 변위되기 때문에) 공기의 절대 투자율은 μ 진공과 거의 같습니다(자기 상수 읽기). 공기의 경우 mu는 1보다 약간 큽니다.