단상 교류

교류 획득

자석의 두 극이 형성하는 자속 속에서 A 도선을 시계 방향으로 회전시키면(Fig. 1), 도선이 자기력선과 교차할 때 e.d. s 값은 식에 의해 결정됩니다.

E = Blvsinα,

여기서 B는 T의 자기 유도, l은 와이어의 길이(m), v는 와이어의 속도(m/s), α는 와이어가 자기장 라인을 가로지르는 각도입니다.

이 경우 B, I 및 v를 일정하게 유지하면 유도된 e가 됩니다. 등. c. 와이어가 자기장을 가로지르는 각도 α에만 의존합니다. 따라서 지점 1에서 와이어가 자기장 라인을 따라 이동할 때 유도된 EMF의 값입니다. 등. 와이어가 포인트 3 oe로 이동할 때 p는 0이 됩니다. 등. v. 힘의 선이 도체에 수직인 방향으로 교차하기 때문에 가장 중요합니다. 등. v. 와이어가 포인트 5로 이동하면 다시 0에 도달합니다.

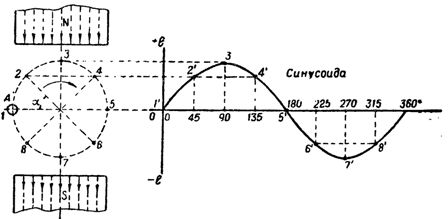
쌀. 1. 유도 e를 변경합니다. 등. 자기장에서 회전하는 와이어에서 pp.

전선이 각도 α = 45 °에서 힘의 선을 교차하는 중간 지점 2와 4에서 유도 기전력의 값. 등. c.는 점 3보다 상응하게 작을 것입니다. 등. v. 0에서 최대로 그리고 다시 0으로 변경합니다.

180 °의 각도를 통해 와이어 A의 추가 회전에서 (지점 6, 7, 8 및 1을 통해) 유도 e의 변화 특성이 분명합니다. 등. p.는 동일하지만 와이어가 이미 다른 극 아래에 있는 자기장 선을 가로지르기 때문에 방향이 반대 방향으로 변경되며 이는 반대 방향의 첫 번째 방향으로 교차하는 것과 같습니다.

따라서 와이어를 360° 회전시키면 e가 유도된다. 등. v. 항상 크기가 변할 뿐만 아니라 방향도 두 번 바뀝니다.

와이어가 약간의 저항에 닫히면 와이어가 나타납니다. 전기, 또한 크기와 방향이 다양합니다.

크기와 방향이 계속 변하는 전류를 교류라고 합니다.

사인파란 무엇입니까?

변경의 성격 e. 등. (전류) 명확성을 높이기 위해 와이어를 한 번 돌리면 곡선을 사용하여 그래픽으로 표시됩니다. e의 값부터. 등. c. sinα에 비례하고 특정 각도를 설정하면 테이블을 사용하여 각 각도의 사인 값을 결정하고 적절한 척도에서 e의 변화에 ​​대한 곡선을 구성할 수 있습니다. 등. c. 이를 위해 수평축에서 와이어의 회전 각도를 따로 설정하고 수직축에서 적절한 스케일로 유도된 e를 설정합니다. 등. ~와 함께

이전에 그림에 표시된 경우.1 부드러운 곡선으로 포인트를 연결하면 유도된 e의 변화의 크기와 특성에 대한 아이디어를 얻을 수 있습니다. 등. (전류) 자기장 내 도체의 모든 위치에서. 유도된 e의 값 때문입니다. 등. p.는 임의의 순간에 와이어가 그림에 표시된 자기장을 가로지르는 각도의 사인에 의해 결정됩니다. 1 곡선을 정현파라고 하며, e. 등. s. - 정현파.

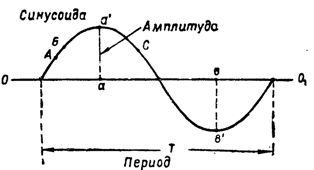
쌀. 2. 정현파와 그 특성값

우리가 살펴본 변경 사항 e. 등. c. 정현파는 360° 각도의 자기장에서 와이어의 회전에 해당합니다. 와이어가 다음 360° 회전하면 유도된 e의 변화가 발생합니다. 등. s.(및 전류)는 사인파에 다시 나타납니다. 즉, 주기적으로 반복됩니다.

따라서 이로 인해 e. 등. c. 전류 정현파 교류... 폐쇄 된 외부 회로가있는 상태에서 와이어 A의 끝에서 측정 할 수있는 전압도 정현파 방식으로 변경된다는 것이 분명합니다.

자속 또는 코일에 연결된 전선 시스템에서 전선을 회전시켜 얻은 교류를 단상 교류라고합니다.

정현파 교류는 기술에서 가장 널리 사용됩니다. 그러나 사인 법칙에 따라 변하지 않는 교류를 찾을 수 있습니다. 이러한 교류를 비정현파라고 합니다.

또한보십시오: 교류란 무엇이며 직류와 어떻게 다릅니까?

단상 교류의 진폭, 주기, 주파수

현재 강도, 정현파를 따라 변화하며 지속적으로 변화합니다. 따라서 지점 A(그림 2)에서 전류가 3a이면 지점 B에서 이미 더 커질 것입니다.정현파의 다른 지점, 예를 들어 지점 C에서 전류는 이제 새로운 값을 갖게 됩니다.

정현파를 따라 변하는 특정 시간의 전류 강도를 순간 전류 값이라고 합니다.

단상 교류의 최대 순시 값은 정현파 진폭을 따라 변할 때 호출됩니다. 와이어를 한 번 돌리면 전류가 진폭 값에 두 번 도달한다는 것을 쉽게 알 수 있습니다. aa'의 값 중 하나는 양수이고 001축으로부터 끌어올려지고 다른 bv'는 음수이고 축으로부터 끌어내려진다.

유도된 시간 e. 등. (또는 현재 힘)은 소위 월간 주기 T(그림 2)라고 하는 전체 변경 주기를 거칩니다. 기간은 일반적으로 초 단위로 측정됩니다.

주기의 역수를 주파수(f)라고 합니다. 다시 말해서, 교류 주파수 단위 시간당 기간 수, 즉 몇 초 만에. 예를 들어, 1초 이내의 교류가 동일한 값과 방향을 10번 가정하면 그러한 교류의 주파수는 초당 10주기가 됩니다.

주파수를 측정하기 위해 초당 주기 수 대신 헤르츠(hertz)라는 단위를 사용합니다. 1Hz의 주파수는 1lps/초의 주파수와 같습니다. 고주파를 측정할 때는 헤르츠보다 1000배 큰 단위, 즉 킬로헤르츠(kHz) 또는 헤르츠보다 1,000,000배 큰 — 메가헤르츠(mhz).

기술에 사용되는 교류는 주파수에 따라 저주파 전류와 고주파 전류로 나눌 수 있다.

AC rms 값

전선을 통과하는 직류가 전선을 가열합니다. 전선을 통해 교류 전류를 흐르게 하면 전선도 가열됩니다.교류는 항상 방향을 바꾸지만 열 방출은 전선의 전류 방향에 전혀 의존하지 않기 때문에 이해할 수 있습니다.

전구에 교류 전류가 흐르면 전구의 필라멘트가 빛납니다. 50Hz의 표준 교류 주파수에서는 열 관성이 있는 백열 전구의 필라멘트가 회로의 전류가 0일 때 냉각할 시간이 없기 때문에 빛이 깜박이지 않습니다. 조명에 50Hz 미만의 주파수를 갖는 교류 전류를 사용하는 것은 전구 강도의 불쾌하고 눈에 피로한 변동이 나타나기 때문에 이제 바람직하지 않습니다.

직류 비유를 계속하면 와이어를 통해 흐르는 교류가 주변에 생성되는 것을 기대할 수 있습니다. 자기장. 실제로 n교류는 자기장을 생성하지 않지만 생성하는 자기장의 방향과 크기도 가변적이기 때문입니다.

교류는 크기와 방향 모두에서 항상 변합니다NS. 당연히 변수 T를 잘 측정하는 방법과 정현파를 따라 변할 때 그 값이 이것 또는 저 동작을 일으키는 것으로 간주되어야 하는가에 대한 질문이 발생합니다.

C 이를 위해 교류는 생성하는 동작의 관점에서 실험 중에 값이 변하지 않는 직류와 비교됩니다.

일정한 저항 10A의 와이어를 통해 직류가 흐르고 와이어가 50 °의 온도로 가열되는 것으로 나타났습니다.이제 동일한 와이어를 통과하면 직류가 아니라 교류이므로 와이어도 50 °의 온도로 가열되도록 값을 선택합니다 (예 : 가변 저항으로 작동). 이 경우 교류의 작용이 직류의 작용과 같다고 말할 수 있습니다.

두 경우 모두 와이어를 동일한 온도로 가열하면 교류가 단위 시간에 직류와 동일한 양의 열을 와이어에서 방출한다는 것을 알 수 있습니다.

단위 시간당 주어진 저항에 대해 직류와 동일한 양의 열을 방출하는 교류 정현파 전류... 이 전류 값을 유효 (Id) 또는 교류의 유효 값이라고합니다 .. . 따라서 우리의 예에서 교류의 유효 값은 10A... 이 경우 최대 (피크) 전류 값은 크기의 평균값을 초과합니다.

경험과 계산에 따르면 교류의 유효 값은 √2 (1.41) 배의 진폭 값보다 작습니다. 따라서 전류의 피크 값을 알면 전류 Id의 유효 값은 전류 Ia의 진폭을 √2로 나누어 결정할 수 있습니다. 즉, Id = Aza/√2

반대로 전류의 rms 값을 알면 전류의 피크 값을 계산할 수 있습니다. 즉, Ia = Azd√2

동일한 관계가 e의 진폭과 rms 값에 대해 유지됩니다. 등. v. 및 전압: 단위 = Ea /√2, Ud = Uа/√2

측정 장치는 대부분 실제 값을 표시하므로 표기할 때 일반적으로 색인 «d»를 생략하지만 잊지 말아야 합니다.

AC 회로의 임피던스

인덕턴스 및 커패시턴스 소비자가 AC 회로에 연결되면 활성 및 리액턴스를 모두 고려해야 합니다(리액턴스는 커패시터가 켜져 있거나 AC 회로의 초크). 따라서 이러한 소비자를 통과하는 전류를 결정할 때 공급 전압을 회로(소비자)의 임피던스로 나눌 필요가 있습니다.

단상 AC 회로의 임피던스(Z)는 다음 공식에 의해 결정됩니다.

Z = √(R2 + (ωL — 1 / ωC)2

여기서 R은 회로의 활성 저항(옴 단위), L은 회로의 인덕턴스(헨리 단위), C는 회로(커패시터)의 정전 용량(패럿 단위), ω - 교류의 각 주파수입니다.

R, L, C의 세 가지 값 또는 그 중 일부만 고려해야 하는 교류 회로에는 서로 다른 소비자가 사용됩니다. 동시에 교류의 각 주파수를 고려해야 합니다.

일부 사용자의 경우 해당 코너 주파수 값에서 R 및 L 값만 고려할 수 있습니다.예를 들어 AC 주파수 50Hz에서 솔레노이드 코일 또는 발전기 권선은 능동 및 유도 저항을 포함하는 것으로만 간주될 수 있습니다. 즉, 이 경우 커패시턴스는 무시할 수 있습니다. 그런 다음 해당 사용자의 AC 임피던스는 다음 공식으로 계산할 수 있습니다.

Z = √(R2 + ω2L2)

이러한 코일이나 교류 동작용으로 설계된 코일을 같은 전압의 직류에 연결하면 매우 큰 전류가 코일을 통해 흐르게 되어 상당한 열이 발생할 수 있으며 코일의 절연이 손상될 수 있습니다. 반대로 직류 회로에서 작동하도록 설계된 코일과 동일한 전압의 교류 회로에 연결된 코일에는 작은 전류가 흐르고 이 코일이 사용되는 장치는 필요한 동작을 수행하지 않습니다.

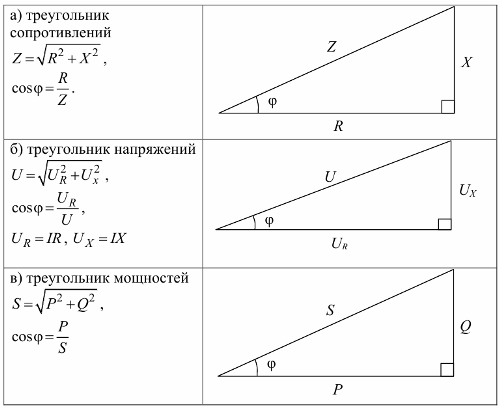
저항 삼각형, 전압 삼각형 및 전력 삼각형: